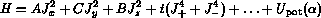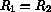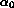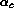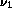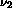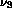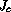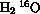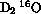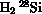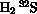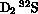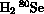Les étudiants se répartissent en groupes de deux personnes. Chaque groupe
aborde le problème commun avec une méthode spécifique. On commence par
une présentation théorique, un mini-colloque avec Dmitrií Sadovskií et Boris Zhilinskií, où chaque
groupe aura 10 minutes pour explique son problème et surtout les méthodes
de solution. Auprès on travaille individuellement en utilisant les moyennes
informatiques. Pendent cet étape on peut contacter le responsable de modul.
On presente les résultat en forme d'un petit rapport fait par chaque groupe.
Il faut utiliser les idées vues en cours de Mécanique Quantique de
maîtrise avec Boris Zhilinskií et en TD
avec Dmitrií Sadovskií.
Les notes sur se module sont annocées ensemble avec celles de
mécanique quantique et physique atomique.
Ces problèmes sont developpés avec participation de
Christophe Van-Hecke.
L'idée générale du module est d'obtenir le maximum des informations sur
le système physique suivant: une particule de masse soumise au potentiel
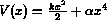
avec le paramètre petit (par rapport à ).
Un premier travail (collectif) doit permettre décrire les caractéristiques
générales du système: structure du spectre d'énergie, comportement du
système avec l'ordre de grandeur des paramètres (cas limites)... .
Dans un second temps, le projet consiste en la résolution numérique de
l'équation de Schroedinger dépendante du temps pour la particule soumise au
potentiel à une dimension décrit ci-dessus. La méthode de résolution
proposée est celle de l'opérateur d'évolution symétrisé. Cette
méthode est présentée dans la référence suivante:
M. D. Feit, J. A. Fleck et A. Steiger,
J. Comp. Phys. 47 (1982), 412-433.
L'élaboration de l'algoritme de propagation à partir de ce document fait
partie intégrante du projet.
Suggestions pour la partie précédent le calcul:
- Est-il possible de réduire le nombre de paramètres du problème?
par changement d'échelle par exemple.
- Le potentiel se réduit-il à un cas plus simple pour certaines
valeurs des paramètres?
- Cette forme de potentiel ne peut-elle être remplacée par une autre
dans le cadre d'une approximation?
- Pourquoi résoudre l'équation de Schrödinger dépendant du
temps? i.e. quelles sont les deux premières caractéristiques d'un
système quantique que l'on cherche souvent à déterminer en premier?
- Où intervient l'aspect numèrique dans la recherche d'informations?
A l'aide de cette méthode, il est demandé d'évaluer les cinquante
premiers niveaux d'énergie du système. Les fonctions qui serviront au
calcul variationnelseront choisies dans la base de fonctions de l'oscillateur
harmonique.
Le projet consiste à calculer pour différentes énergies l'intégrale
d'action du système. Puis, celle-ci étant connue pour la gamme d'énergies
intéressantes (par exemple celle couvrant les cinquante premiers niveaux), on
invoquera le postulat de quantification de Born-Sommerfeld pour déterminer la
position desdits niveaux dénergie.
Lorsque le paramètre du potentiel est petit, la partie
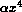 peut être considérée comme une perturbation de l'oscillateur harmonique
associé aux paramètres et . En utilisant la théorie des
perturbations stationnaires, il est demandé de calculer les cinquante
premiers niveaux d'énergie. En option (vivement recommandée), il est
possible d'évaluer les fonctions d'onde correspondantes.
Considérons l'hamiltonien pour le problème de Henon-Heiles, un oscillateur
à 2D dégénéré 1:1 avec un potentiel cubique de symétrie ,
Ces problèmes sont posés autour le Hamiltonien rotationnel-vibrationnel
moleculaire.
peut être considérée comme une perturbation de l'oscillateur harmonique
associé aux paramètres et . En utilisant la théorie des
perturbations stationnaires, il est demandé de calculer les cinquante
premiers niveaux d'énergie. En option (vivement recommandée), il est
possible d'évaluer les fonctions d'onde correspondantes.
Considérons l'hamiltonien pour le problème de Henon-Heiles, un oscillateur
à 2D dégénéré 1:1 avec un potentiel cubique de symétrie ,
Ces problèmes sont posés autour le Hamiltonien rotationnel-vibrationnel
moleculaire.

Considerez une molécule du type BAB:
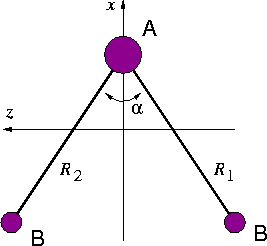
Son Hamiltonien classique rotationnel est
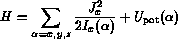 tandis que son Hamiltonien quantique effectif peut être représente
sous forme suivante
tandis que son Hamiltonien quantique effectif peut être représente
sous forme suivante
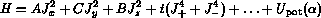
Données sur les molécules de type BAB: distance AB à l'équilibre,
angle BAB à l'équilibre et au point critique, fréquences harmoniques
de trois modes de vibration, valeur critique de moment angulaire
[I.M.Pavlichenkov, Phys. Rep. 226 173-279 (1993)]
|
molécule |
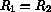 |
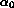 |
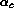 |
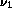 |
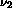 |
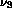 |
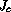 |
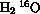 | 0.96 | 104 | 87 | 3657 | 1595 | 3756 | 26 |
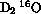 | 0.97 | 104 | 84 | 2672 | 1178 | 2788 | 44 |
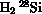 | 1.52 | 93 | 88 | 2032 | 1008 | 2022 | 18 |
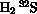 | 1.34 | 92 | 88 | 2615 | 1183 | 2628 | 15 |
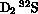 | 1.34 | 92 | 87 | 1910 | 858 | 1922 | 26 |
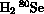 | 1.46 | 91 | 89 | 2345 | 1034 | 2358 | 9 |
|
|
Dmitrií Sadovskií (sadovski@pca3.univ-littoral.fr) October 13, 1998
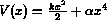
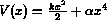
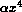 peut être considérée comme une perturbation de l'oscillateur harmonique
associé aux paramètres et . En utilisant la théorie des
perturbations stationnaires, il est demandé de calculer les cinquante
premiers niveaux d'énergie. En option (vivement recommandée), il est
possible d'évaluer les fonctions d'onde correspondantes.
peut être considérée comme une perturbation de l'oscillateur harmonique
associé aux paramètres et . En utilisant la théorie des
perturbations stationnaires, il est demandé de calculer les cinquante
premiers niveaux d'énergie. En option (vivement recommandée), il est
possible d'évaluer les fonctions d'onde correspondantes.

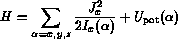 tandis que son Hamiltonien quantique effectif peut être représente
sous forme suivante
tandis que son Hamiltonien quantique effectif peut être représente
sous forme suivante